1.
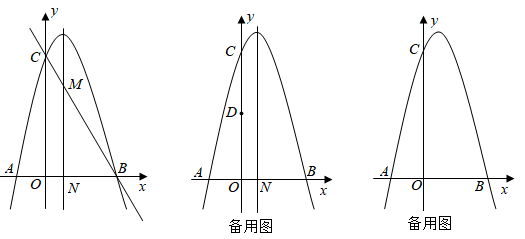
如图,一次函数 的图象与坐标轴交于点A、B,二次函数
的图象与坐标轴交于点A、B,二次函数 的图象过A、B两点.
的图象过A、B两点.

(1)
求二次数的表达式
(2)
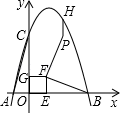
已知点 在对称轴上,且点
在对称轴上,且点 位于
位于 轴上方,连接
轴上方,连接 , 若
, 若 , 求P的坐标
, 求P的坐标
【考点】
待定系数法求二次函数解析式;