在菱形ABCD中，， P是直线BD上一动点，以AP为边向右侧作等边（A ， P ， E按逆时针排列），点E的位置随点P的位置变化而变化. 图1 图2 图3

0 返回出卷网首页

1. 在菱形ABCD中， $\text{[math]}$ ， P是直线BD上一动点，以AP为边向右侧作等边 $\text{[math]}$ （A ， P ， E按逆时针排列），点E的位置随点P的位置变化而变化.

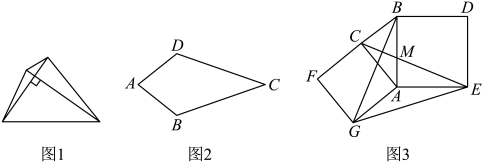
图1 图2 图3

(1) 如图1，当点P在线段BD上，且点E在菱形ABCD内部或边上时，连接CE ，则BP与CE的数量关系是，AD与CB的位置关系是；

(2) 如图2，当点P在段BD上，且点E在菱形ABCD外部时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由；

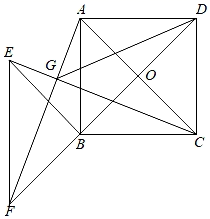
(3) 当点P在直线BD上时，其他条件不变，连接BE.若 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的面积.

【考点】

三角形全等及其性质; 等边三角形的性质; 勾股定理; 菱形的性质; 四边形的综合;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图1，我们把对角线互相垂直的四边形叫做垂美四边形．

(1) 概念理解：我们已经学习了平行四边形、菱形、矩形、正方形，在这四种图形中是垂美四边形的是．

(2) 性质探究：如图2，已知四边形 $\text{[math]}$ 是垂美四边形，求证： $\text{[math]}$ ．

(3) 问题解决：如图3，分别以 $\text{[math]}$ 的直角边 $\text{[math]}$ 和斜边 $\text{[math]}$ 为边向外作正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

综合题困难

2. 如图，在正方形ABCD中，对角线AC与BD相交于点O，以B为顶点的等腰Rt△BEF绕点B旋转，连接AF与CE相交于点G，连接DG．

(1) 求证：CE⊥AF；

(2) 求证：AG＋CG＝ $\text{[math]}$ DG；

(3) 连接CF，当EG∶AG∶FG＝l∶2∶5，且S正方形ABCD＝100时，求DG的长和△BCF的面积．

综合题困难

3. 如图，在平面直角坐标系中，菱形ABCD的顶点A，B的坐标分别为（﹣6，0），（4，0），点D在y轴上．

(1) 求点C的坐标；

(2) 求对角线AC的长．

综合题普通