1.


(1)
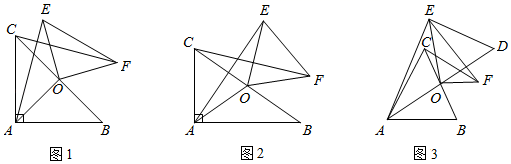
【案例展示】如图 , 点
, 点 、
、 分别在正方形
分别在正方形 的边
的边 、
、 上,
上, , 连接
, 连接 , 则
, 则 , 理由如下:
, 理由如下:
 , 可把
, 可把 绕点
绕点 逆时针旋转
逆时针旋转 至
至 , 可使
, 可使 与
与 重合,
重合,
 ,
,
 , 点
, 点 、
、 、
、 共线,由旋转得:
共线,由旋转得: ≌
≌ ,
,
 ,
,  ,
,  , 而
, 而 ,
,
 , 即
, 即 ,
,
 ≌
≌ , 根据是
, 根据是 第一空填三角形,第二空填全等的依据
第一空填三角形,第二空填全等的依据 ,
,
 ,
,
又 ,
,
 .
(2)
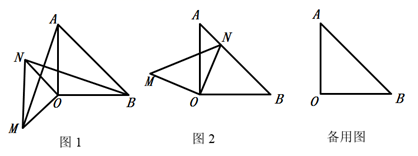
【类比引申】如图
.
(2)
【类比引申】如图 , 四边形
, 四边形 中,
中, ,
,  点
点 、
、 分别在边
分别在边 、
、 上,
上, 若
若 、
、 都不是直角时
都不是直角时 仍成立,则
仍成立,则 与
与 应该满足什么数量关系是.
(3)
【拓展运用】如图
应该满足什么数量关系是.
(3)
【拓展运用】如图 , 在
, 在 中,
中, ,
,  , 点
, 点 、
、 均在边
均在边 上,且
上,且 猜想
猜想 、
、 、
、 应满足的等量关系,并写出推理过程.
应满足的等量关系,并写出推理过程.
又
【考点】
勾股定理;
旋转的性质;
三角形全等的判定-SAS;
能力提升
真题演练