1.
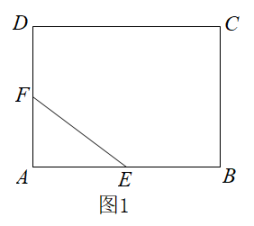
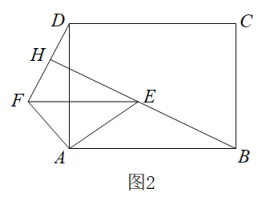
综合与实践:如图1,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”.如图2,在 中,
中, , 将线段
, 将线段 绕点
绕点 顺时针旋转
顺时针旋转 得到线段
得到线段 , 作
, 作 交
交 的延长线于点
的延长线于点 .
.

(1)
【观察感知】如图2,通过观察,线段 与
与 的数量关系是______;
(2)
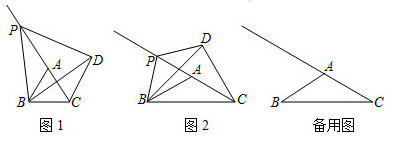
【问题解决】如图3,连接
的数量关系是______;
(2)
【问题解决】如图3,连接 并延长交
并延长交 的延长线于点
的延长线于点 , 若
, 若 ,
,  , 求
, 求 的面积;
(3)
【类比迁移】在(2)的条件下,连接
的面积;
(3)
【类比迁移】在(2)的条件下,连接 交
交 于点
于点 , 则
, 则 ______;
(4)
【拓展延伸】在(2)的条件下,在直线
______;
(4)
【拓展延伸】在(2)的条件下,在直线 上找点
上找点 , 使
, 使 , 请直接写出线段
, 请直接写出线段 的长度.
的长度.
【考点】
相似三角形的判定与性质;
解直角三角形;
旋转的性质;
能力提升
真题演练