1.
定义:在平面直角坐标系中,直线 与某函数图象交点记为点P,作该函数图象中,点P及点P右侧部分关于直线
与某函数图象交点记为点P,作该函数图象中,点P及点P右侧部分关于直线 的轴对称图形,与原函数图象上的点P及点P右侧部分共同构成一个新函数的图象,称这个新函数为原函数关于直线
的轴对称图形,与原函数图象上的点P及点P右侧部分共同构成一个新函数的图象,称这个新函数为原函数关于直线 的“迭代函数”.例如:图1是函数
的“迭代函数”.例如:图1是函数 的图象,则它关于直线
的图象,则它关于直线 的“迭代函数”的图象如图2所示,可以得出它的“迭代函数”的解析式为
的“迭代函数”的图象如图2所示,可以得出它的“迭代函数”的解析式为 .
.

(1)
写出函数 关于直线
关于直线 的“迭代函数”的解析式为_________.
(2)
若函数
的“迭代函数”的解析式为_________.
(2)
若函数 关于直线
关于直线 的“迭代函数”图象经过
的“迭代函数”图象经过 , 则
, 则 _________.
(3)
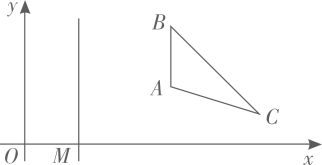
以如正方形
_________.
(3)
以如正方形 的顶点分别为:
的顶点分别为:
, 其中
.
①若函数关于直线
的“迭代函数”的图象与正方形
的边有3个公共点,则
______;
②若 , 函数
关于直线
的“迭代函数”的图象与正方形
有4个公共点,则n的取值范围为______.
【考点】
坐标与图形变化﹣对称;