1.
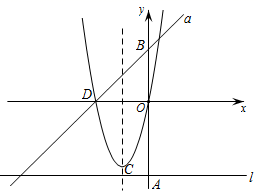
如图,抛物线 与x轴交于点
与x轴交于点 和点B , 与y轴交于点
和点B , 与y轴交于点 , 其顶点为D .
, 其顶点为D .

(1)
求抛物线的表达式及顶点D的坐标;
(2)
在y轴上是否存在一点M , 使得 的周长最小.若存在,求出点M的坐标;若不存在,请说明理由;
(3)
若点E在以点
的周长最小.若存在,求出点M的坐标;若不存在,请说明理由;
(3)
若点E在以点 为圆心,1为半径的⊙P上,连结AE , 以AE为边在AE的下方作等边三角形AEF , 连结BF . 求BF的取值范围.
为圆心,1为半径的⊙P上,连结AE , 以AE为边在AE的下方作等边三角形AEF , 连结BF . 求BF的取值范围.
【考点】
轴对称的应用-最短距离问题;
二次函数-动态几何问题;
二次函数-线段周长问题;
能力提升