如图，在四边形ABCD中，AD∥BC，∠B＝90°，AB＝8cm，AD＝12cm，BC＝18cm，点P从点A出发以1cm/s的速度向点D运动；点Q从点C同时出发，以2cm/s的速度向点B运动，当点Q到达点B时，点P也停止运动，设点P，Q运动的时间为ts．

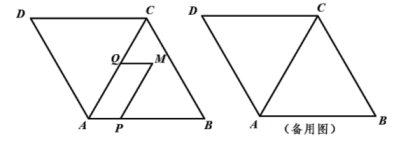
1. 如图，在四边形ABCD中，AD∥BC，∠B＝90°，AB＝8cm，AD＝12cm，BC＝18cm，点P从点A出发以1cm/s的速度向点D运动；点Q从点C同时出发，以2cm/s的速度向点B运动，当点Q到达点B时，点P也停止运动，设点P，Q运动的时间为ts．

(1) 从运动开始，当t取何值时，PQ∥CD？

(2) 在整个运动过程中是否存在t值，使得四边形PQCD是菱形？若存在，请求出t值；若不存在，请说明理由；

(3) 从运动开始，当t取何值时，四边形PQBA是矩形？

(4) 在整个运动过程中是否存在t值，使得四边形PQBA是正方形？若存在，请求出t值；若不存在，请说明理由．

【考点】

平行四边形的判定与性质; 菱形的性质; 矩形的判定与性质; 正方形的判定; 四边形-动点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

解答题困难

解答题困难

3. 如图，在菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ 过点 $\text{[math]}$ 作 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．

解答题普通