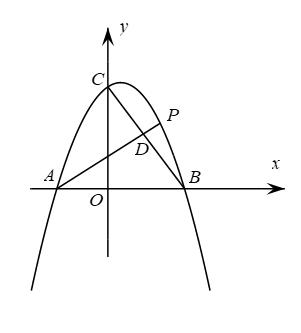
如图1，在平面直角坐标系中，抛物线与轴交于A、B两点，与轴交于点C．

0 返回出卷网首页

1. 如图1，在平面直角坐标系中，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于A、B两点，与 $\text{[math]}$ 轴交于点C．

(1) 求点A、B、C的坐标；

(2) 如图2，若点P在以点O为圆心， $\text{[math]}$ 长为半径作的圆上，连接 $\text{[math]}$ ，请你直接写出 $\text{[math]}$ 的最小值．

【考点】

二次函数图象与坐标轴的交点问题; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 的顶点为A．

(1) 如图1，若A点横坐标为1，点 $\text{[math]}$ 在抛物线M上，求t的值；

(2) 如图2，若 $\text{[math]}$ ，直线 $\text{[math]}$ ，求b变化时点A到直线l的距离最小值；

(3) 若 $\text{[math]}$ ，当 $\text{[math]}$ 时 $\text{[math]}$ ，求a的取值范围．

解答题困难

2. 如图，抛物线 $\text{[math]}$ 与x轴交于点A，点B，与y轴交于点C．抛物线的对称轴为直线 $\text{[math]}$ ，点C坐标为 $\text{[math]}$ ．

(1) 求抛物线表达式；

(2) 在抛物线上是否存在点P，使 $\text{[math]}$ ，如果存在，求出点P坐标；如果不存在，请说明理由；

(3) 在（2）的条件下，若点P在x轴上方，点M是直线 $\text{[math]}$ 上方抛物线上的一个动点，求点M到直线 $\text{[math]}$ 的最大距离．

解答题困难

3. 抛物线 $\text{[math]}$ 交x轴于A，B两点（A在B的左边），C是第一象限抛物线上一点，直线 $\text{[math]}$ 交y轴于点P．

(1) 直接写出A，B两点的坐标；

(2) 如图①，当 $\text{[math]}$ 时，在抛物线上存在点D（异于点B），使B，D两点到 $\text{[math]}$ 的距离相等，求出所有满足条件的点D的横坐标；

(3) 如图②，直线 $\text{[math]}$ 交抛物线于另一点E，连接 $\text{[math]}$ 交y轴于点F，点C的横坐标为m，求 $\text{[math]}$ 的值（用含m的式子表示）．

解答题困难