1.
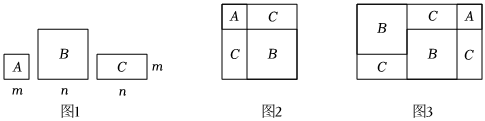
数学活动课上,老师准备了若干个如图1的三种纸片(其中A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是边长分别为a、b的长方形),并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.

(1)
观察图2,请你写出下列三个代数式: 之间的等量关系:__________.
(2)
若要拼出一个面积为
之间的等量关系:__________.
(2)
若要拼出一个面积为 的矩形,则需要A号卡片__________张,B号卡片__________张,C号卡片__________张;
(3)
根据(1)中得出的等量关系,解决如下问题:已知
的矩形,则需要A号卡片__________张,B号卡片__________张,C号卡片__________张;
(3)
根据(1)中得出的等量关系,解决如下问题:已知 , 求
, 求 的值;
(4)
两个正方形
的值;
(4)
两个正方形 ,
,  如图3摆放,边长分别为x,y.若
如图3摆放,边长分别为x,y.若 , 则图中阴影部分面积的和为__________.
, 则图中阴影部分面积的和为__________.
【考点】
多项式乘多项式;
完全平方公式的几何背景;
能力提升