正方形中，， E是中点，M为线段上一点（不与D，E重合），连接．

0 返回出卷网首页

1. 正方形 $\text{[math]}$ 中， $\text{[math]}$ ， E是 $\text{[math]}$ 中点，M为线段 $\text{[math]}$ 上一点（不与D，E重合），连接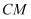 $\text{[math]}$ ．

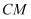(1) 如图，将线段 $\text{[math]}$ 绕点C逆时针旋转 $\text{[math]}$ 得 $\text{[math]}$ ，连接 $\text{[math]}$ ．求证： $\text{[math]}$ ；

(2) 若M为 $\text{[math]}$ 的中点，在（1）的条件下，求 $\text{[math]}$ 的长．

【考点】

三角形全等及其性质; 勾股定理; 正方形的性质; 旋转的性质; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. （1）如图1，点C是线段 $\text{[math]}$ 上的点，在 $\text{[math]}$ 上方作等边三角形 $\text{[math]}$ ，连接 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是．

（2）如图2，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点E是边 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，将边 $\text{[math]}$ 绕点C顺时针旋转，点B的对应点F落在 $\text{[math]}$ 上，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为多少?

（3）如图3，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ，点E为 $\text{[math]}$ 上一点， $\text{[math]}$ ，将 $\text{[math]}$ 绕着点A逆时针旋转，得到 $\text{[math]}$ ，点E的对应点为G，连接 $\text{[math]}$ ，取 $\text{[math]}$ 的中点M，连接 $\text{[math]}$ ．若在旋转过程中，点M恰好落在 $\text{[math]}$ 边上，求此时 $\text{[math]}$ 的面积．

解答题普通

2. 我们可以通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的，下面是一个案例，请补充完整

原题：如图 $\text{[math]}$ ，点 $\text{[math]}$ 分别在正方形 $\text{[math]}$ 的边 $\text{[math]}$ 上， $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ ，试说明理由．

(1) 思路梳理

∵ $\text{[math]}$ ，

∴把 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 至 $\text{[math]}$ ，可使 $\text{[math]}$ 与 $\text{[math]}$ 重合．

∵ $\text{[math]}$ ，

∴ $\text{[math]}$ ，点 $\text{[math]}$ 共线．

根据三角形全等的判定定理 $\text{[math]}$ 中的________________，易证： $\text{[math]}$ ________________，得 $\text{[math]}$ ；

(2) 类比引申

如图 $\text{[math]}$ ，四边形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 分别在边 $\text{[math]}$ 上， $\text{[math]}$ ．若 $\text{[math]}$ 都不是直角，则当 $\text{[math]}$ 与 $\text{[math]}$ 满足等量关系________________时，仍有 $\text{[math]}$ ；

(3) 联想拓展

如图 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 均在边 $\text{[math]}$ 上，且 $\text{[math]}$ ．猜想 $\text{[math]}$ 应满足的等量关系，并写出推理过程．

解答题困难

3. （1）阅读理解：如图1，在正方形 $\text{[math]}$ 中，若 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 边上的点， $\text{[math]}$ ，则我们常会想到：把 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，易证 $\text{[math]}$ ______，得出线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系为______；

（2）类比探究：如图2，在等边 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上的点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求线段 $\text{[math]}$ 的长；

（3）拓展应用：如图3，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 在 $\text{[math]}$ 边上， $\text{[math]}$ ，若 $\text{[math]}$ 是等腰 $\text{[math]}$ 的腰长，请求出 $\text{[math]}$ 的值．

解答题困难