1.


(1)
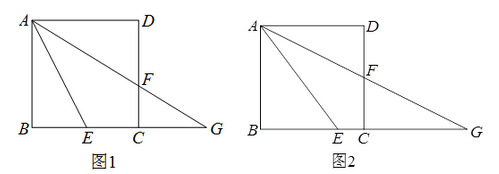
发现: 如图①所示, 在正方形ABCD中, 点E, F分别是AB, AD上的两点, 连接DE, CF,DE⊥CF. 则  (2)
探究:如图②,在矩形ABCD中, E为AD边上一点,且
(2)
探究:如图②,在矩形ABCD中, E为AD边上一点,且  将
将  沿BE 翻折到
沿BE 翻折到  处, 延长EF交BC边于G点, 延长BF交CD边于点H, 且
处, 延长EF交BC边于G点, 延长BF交CD边于点H, 且  ①求CH 的长; ②求AE的长.
(3)
拓展:如图③,在菱形ABCD中, AB=6, E为CD边上的一点且
①求CH 的长; ②求AE的长.
(3)
拓展:如图③,在菱形ABCD中, AB=6, E为CD边上的一点且  沿AE翻折得到△AFE, AF 与CD交于H且
沿AE翻折得到△AFE, AF 与CD交于H且  直线EF交直线BC于点 P, 求 PE 的长.
直线EF交直线BC于点 P, 求 PE 的长.
【考点】
勾股定理;
菱形的性质;
矩形的性质;
正方形的性质;
三角形全等的判定-AAS;
全等三角形中对应边的关系;
相似三角形的判定-AA;
相似三角形的性质-对应边;