1.
在等腰 中,
中, ,
,  .
.

(1)
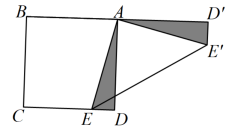
如图1,D,E是等腰 斜边
斜边 上两动点,且
上两动点,且 °,将
°,将 绕点A逆时针旋转90°后,得到
绕点A逆时针旋转90°后,得到 , 连接
, 连接 .
(2)
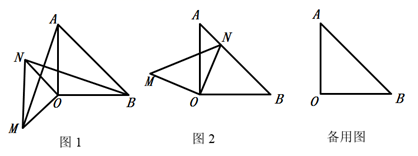
如图2,点D是等腰
.
(2)
如图2,点D是等腰 斜边
斜边 所在直线上的一动点,连接
所在直线上的一动点,连接 , 以点A为直角顶点顺时针作等腰
, 以点A为直角顶点顺时针作等腰 , 当
, 当 ,
,  时,直接写出
时,直接写出 的长.
的长.
①求证:;
②试判断、
、
三条线段之间的关系,并说明理由.
【考点】
勾股定理;
旋转的性质;
三角形全等的判定-SAS;