1.
数学是以数量关系和空间形式为主要研究对象的科学．数学实践活动有利于我们在图形运动变化的过程中去发现其中的位置关系和数量关系，让我们在学习与探索中发现数学的静态美和动态美，掌握运动中的不变量和应变量，体会数学实践活动带给我们的乐趣．
一般情形下，我们常说旋转与翻折是伴随的．
(1)
其实翻折可以近似看作是旋转的一种，请简要描述理由：
(2)
如图①，在矩形
中，点E、F、G分别为边
、
、
的中点，连接
、
， H为的中点，连接
． 将
绕点B旋转，线段、和
的位置和长度也随之变化．当绕点B顺时针旋转
时，请解决下列问题：
(3)
在
的条件下，连接图③中矩形的对角线
， 并沿对角线剪开，得
（如图④)．点M、N分别在、上，连接
， 将
沿翻折，使点C的对应点P落在的延长线上，若
平分
， 求：
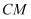的长．
_______________________________________________________________________．
图②中，
， 此时点E落在
的延长线上，点F落在线段
上，连接
， 猜想
与
之间的数量关系，并证明你的猜想从特殊到一般，也是数学几何思考的重要方法：
图③中，
， 则
；
当
时，
．
【考点】
勾股定理;
相似三角形的判定与性质;
解直角三角形;
旋转的性质;
能力提升
