1.
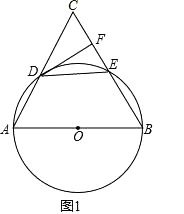
如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D , DF是圆的切线,过点F作BC的垂线交BC于点G .


(1)
求证:DF⊥AB;
(2)
若AF的长为2,求FG的长
【考点】
等边三角形的判定与性质;
切线的性质;
圆与三角形的综合;