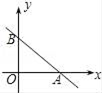
1.
作出函数 的图象,并回答下列问题:
的图象,并回答下列问题:

(1)
函数图象与 轴,
轴, 轴分别交于点A、B,则点
轴分别交于点A、B,则点 的坐标为,点B的坐标为;
(2)
求原点到此函数图象的距离;
(3)
在直线
的坐标为,点B的坐标为;
(2)
求原点到此函数图象的距离;
(3)
在直线 上是否存在动点P,使
上是否存在动点P,使 的面积为12,若存在,求出点P的坐标,若不存在,请说明理由.
的面积为12,若存在,求出点P的坐标,若不存在,请说明理由.
【考点】
一次函数的图象;
三角形的面积;
勾股定理的应用;
一次函数图象与坐标轴交点问题;
能力提升