1.
已知, , 分别在边OP,OQ上取点A,B,使
, 分别在边OP,OQ上取点A,B,使 , 过点
, 过点 平行于OQ的直线与过点
平行于OQ的直线与过点 平行于OP的直线相交于点
平行于OP的直线相交于点 . 点E,F分别是射线OP,OQ上动点,连接CE,CF,EF.
. 点E,F分别是射线OP,OQ上动点,连接CE,CF,EF.

(1)
求证: ;
(2)
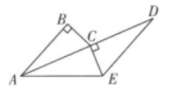
如图1,当点E,F分别在线段AO,BO上,且
;
(2)
如图1,当点E,F分别在线段AO,BO上,且 时,请求出线段EF,AE,BF之间的等量关系式;
(3)
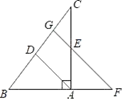
如图2,当点E,F分别在AO,BO的延长线上,且
时,请求出线段EF,AE,BF之间的等量关系式;
(3)
如图2,当点E,F分别在AO,BO的延长线上,且 时,延长AC交EF于点
时,延长AC交EF于点 , 延长BC交EF于点
, 延长BC交EF于点 . 请猜想线段EN,NM,FM之间的等量关系,并证明你的结论.
. 请猜想线段EN,NM,FM之间的等量关系,并证明你的结论.
【考点】
平行线的性质;
三角形全等及其性质;
三角形全等的判定;
等腰三角形的性质;
勾股定理;