0 返回出卷网首页
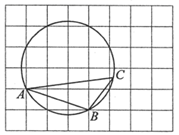
1. 如图，在每个小正方形的边长为1的网格中， 的顶点A ， B均在格点上， ，经过A ， B ， C三点的圆的半径为 ．

(1) 线段 的长等于；
(2) 请用无刻度的直尺，在如图所示的网格中，画出一个点P ， 使其满足 ，并简要说明点P的位置是如何找到的（不要求证明）
【考点】
三角形全等及其性质; 三角形全等的判定; 勾股定理;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，在▱ABCD中，点E，F在对角线AC上，且AE=CF．求证：

(1) DE=BF；
(2) 四边形DEBF是平行四边形．
综合题 普通
2. ∆ABC中，点D在直线AB上.点E在平面内，点F在BC的延长线上，∠E=∠BDC，AE=CD，∠EAB+∠DCF=180º．

(1) 如图①，求证AD+BC=BE；
(2) 如图②、图③，请分别写出线段AD，BC，BE之间的数量关系，不需要证明；
(3) 若BE⊥BC，tan∠BCD= ，CD=10，则AD=．
综合题 困难
3. 如图①，有一组平行线l1∥l2∥l3∥l4 ， 正方形ABCD的四个顶点分别在l1、l2、l3、l4上，EG过点D且垂直于l1于点E，分别交l2、l4于点F、G，EF＝DG＝1，DF＝2.

(1) AE＝，正方形ABCD的边长＝；
(2) 如图②，将∠AED绕点A顺时针旋转α°得到∠AE′D′，且0°＜α＜90°，点D′在直线l3上，以AD′为边在E′D′左侧作菱形AD′C′B′，使点B′、C′分别在直线l2、l4上．

①写出∠B′AD′与α的函数关系并给出证明；

②若α＝30°，求菱形AD′C′B′的边长．
综合题 困难