1.
如图,菱形 , 点
, 点 为平面内一点,连接AE.
为平面内一点,连接AE.

(1)
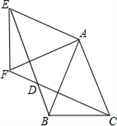
如图1,点 在BC的延长线上,将AE绕点
在BC的延长线上,将AE绕点 顺时针旋转
顺时针旋转 得AF,交EB延长线于点
得AF,交EB延长线于点 , 连接EF交AB延长线于点
, 连接EF交AB延长线于点 , 若
, 若 , 求AE的长;
(2)
如图2,点
, 求AE的长;
(2)
如图2,点 在AC的延长线上,将AE绕点
在AC的延长线上,将AE绕点 逆时针旋转
逆时针旋转 得AF,连接EF,点
得AF,连接EF,点 为CE的中点,连接BM,FM,证明:
为CE的中点,连接BM,FM,证明: ;
(3)
如图3,将AB沿AS翻折得
;
(3)
如图3,将AB沿AS翻折得 , 连DE交AS于点
, 连DE交AS于点 , 点
, 点 为平面内一点,当DS取得最大值时,连接TD,TE,若
为平面内一点,当DS取得最大值时,连接TD,TE,若 , 求
, 求 的最大值.
的最大值.
【考点】
等腰三角形的性质;
勾股定理的应用;
菱形的性质;
旋转的性质;
圆与函数的综合;