1.
如图1,在矩形ABCD中,点E,F分别在AB,BC边上,DE=AF,DE⊥AF于点G.

(1)
求证:四边形ABCD是正方形;
(2)
延长CB到点H,使得BH=AE,判断AAHF的形状,并说明理由
(3)
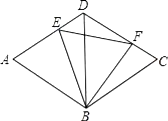
如图2,在菱形ABCD中,点E,F分别在AB,BC边上,DE与AF相交于点G,DE=AF,∠AED=60°,AE=6,BF=2,求DE的长
【考点】
三角形全等及其性质;
三角形全等的判定;
等边三角形的判定与性质;
菱形的性质;
正方形的判定;