已知：在正方形ABCD的边BC上任取一点，连接AF，一条与AF垂直的直线（垂足为点）沿AF方向，从点开始向下平移，交边AB于点．

0 返回出卷网首页

1. 已知：在正方形ABCD的边BC上任取一点 $\text{[math]}$ ，连接AF，一条与AF垂直的直线 $\text{[math]}$ （垂足为点 $\text{[math]}$ ）沿AF方向，从点 $\text{[math]}$ 开始向下平移，交边AB于点 $\text{[math]}$ ．

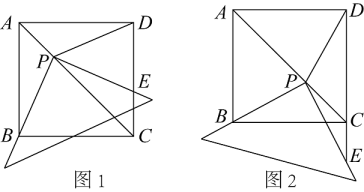
(1) 当直线l经过正方形ABCD的顶点D时，如图1所示．求证：AE＝BF；

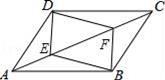
(2) 当直线l经过AF的中点时，与对角线BD交于点Q ，连接FQ ，如图2所示．求∠AFQ的度数；

(3) 直线l继续向下平移，当点P恰好落在对角线BD上时，交边CD于点G ，如图3所

示．设AB＝2，BF＝x ， DG＝y ，求y与x之间的关系式．

【考点】

三角形全等及其性质; 三角形全等的判定; 线段垂直平分线的性质; 正方形的判定与性质; 两条直线被一组平行线所截，所得的对应线段成比例;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 将一块足够大的直角三角板的直角顶点P放在边长为1的正方形ABCD的对角线AC上滑动，一条直角边始终经过点B，另一条直角边与射线DC交于点E.

(1) 当点E在边DC上时（如图1），求证：

①△PBC ≌△PDC；

②PB=PE.

(2) 当点E在边DC的延长线上时（如图2），（1）中的结论②还成立吗？如果不成立，请说明理由；如果成立，请给予证明.

综合题普通

2. 如图，在▱ABCD中，点E，F在对角线AC上，且AE=CF．求证：

(2) 四边形DEBF是平行四边形．

综合题普通

3. ∆ABC中，点D在直线AB上.点E在平面内，点F在BC的延长线上，∠E=∠BDC，AE=CD，∠EAB+∠DCF=180º．

(1) 如图①，求证AD+BC=BE；

(2) 如图②、图③，请分别写出线段AD，BC，BE之间的数量关系，不需要证明；

(3) 若BE⊥BC，tan∠BCD= $\text{[math]}$ ，CD=10，则AD=．

综合题困难