如图1，平面内有一点P到△ABC的三个顶点的距离分别为PA、PB，~PC，若有，则称点为关于点的勾股点．类似地，若，则称点为关于点的勾股点．

0 返回出卷网首页

1. 如图1，平面内有一点P到△ABC的三个顶点的距离分别为PA、PB，~PC，若有 $\text{[math]}$ ，则称点 $\text{[math]}$ 为 $\text{[math]}$ 关于点 $\text{[math]}$ 的勾股点．类似地，若 $\text{[math]}$ ，则称点 $\text{[math]}$ 为 $\text{[math]}$ 关于点 $\text{[math]}$ 的勾股点．

(1) 【知识感知】

如图2，在4×5的网格中，每个小正方形的长均为1，点A、B、C、D、E、F、G均在小正方形的顶点上，则点D是ABC关于点的勾股点；在点E、F、G三点中只有点是ABC关于点A的勾股点

(2) 【知识应用】

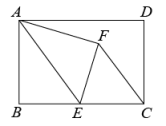
如图3，E是矩形ABCD内一点，且点C是△ABE关于点A的勾股点，求证：CE=CD；

(3) 【知识拓展】

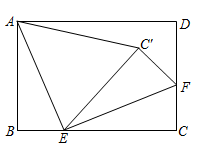
矩形ABCD中，AB=5，BC=6，E是矩形ABCD内一点，且点C是△ABE关于点A的勾股点，若△ADE是等腰三角形，求AE的长．

【考点】

等腰三角形的性质; 勾股定理; 矩形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AM⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．

(1) 【特例探究】

如图1，当tan∠PAB=1，c=4 $\text{[math]}$ 时，a=，b=；

如图2，当∠PAB=30°，c=2时，a=，b=；

(2) 【归纳证明】

请你观察（1）中的计算结果，猜想a²、b²、c²三者之间的关系，用等式表示出来，并利用图3证明你的结论．

(3) 【拓展证明】

如图4，▱ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=3 $\text{[math]}$ ，AB=3，求AF的长．

实践探究题困难

2. 如图， $\text{[math]}$ 为线段AB上一点， $\text{[math]}$ ，射线 $\text{[math]}$ 于点C，P为射线CD上一点，连结PA，PB.

(1) 【发现、提出问题】

①当PC=3时，求 $\text{[math]}$ 的值.

②小亮发现PC取不同值时， $\text{[math]}$ 的值存在一定规律，请猜想该规律： ▲ .

(2) 【分析、解决问题】请证明你的猜想.

(3) 【运用】当 $\text{[math]}$ 时，求 $\text{[math]}$ 的周长.

实践探究题普通