1.
已知∠MAN,AC平分∠MAN.

(1)
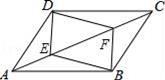
在图1中,若∠MAN=120°,∠ABC=∠ADC=90°,求证:AB+AD=AC;
(2)
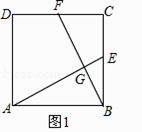
在图2中,若∠MAN=120°,∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)
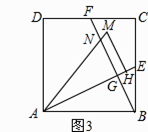
在图3中:①∠MAN=60°,∠ABC+∠ADC=180°,则AB+AD= ▲ AC;
②若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,则AB+AD= ▲ AC(用含α的三角函数表示),并给出证明.
【考点】
三角形全等及其性质;
三角形全等的判定;
角平分线的性质;
含30°角的直角三角形;
求余弦值;