1.
问题情境:数学活动课上,同学们开展了以“矩形纸片折叠”为主题的探究活动(每个小组的矩形纸片规格相同),已知矩形纸片宽 .
.

(1)
动手实践:
(2)
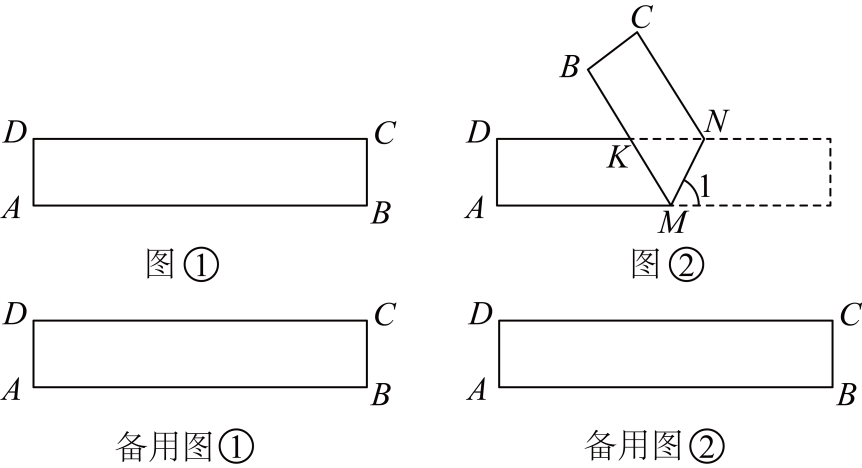
如图2, 小组将矩形纸片ABCD对折使AB与DC重合,展平后得到折痕PQ , 再次过点
小组将矩形纸片ABCD对折使AB与DC重合,展平后得到折痕PQ , 再次过点 折叠使点
折叠使点 落在折痕PQ上的点
落在折痕PQ上的点 处,得到折痕AM , 连结MN , 展平后得到四边形ANMD , 请求出四边形ANMD的面积.
(3)
深度探究:
处,得到折痕AM , 连结MN , 展平后得到四边形ANMD , 请求出四边形ANMD的面积.
(3)
深度探究:
如图1,小组将矩形纸片ABCD折叠,点
落在AB边上的点
处,折痕为AF , 连接EF , 然后将纸片展平,得到四边形AEFD.试判断四边形AEFD的形状,并加以证明.
如图3,小组将图1中的四边形EFCB剪去,然后在边AD , EF上取点G , H , 将四边形AEFD沿GH折叠,使
点的对应点
始终落在边DF上(点
不与点D , F重合),点
落在点
处,
与EF交于点
.
探究①当在DF上运动时,
的周长是否会变化?如变化,请说明理由;如不变,请求出该定值.
探究②直接写出四边形GAEH面积的最小值.
【考点】
三角形全等的判定;
矩形的性质;
翻折变换(折叠问题);
直角三角形的性质;