1.
《几何原本》是数学发展史中的不朽著作,该书记载了很多利用几何图形来论证代数结论的方法,凸显了数形结合的思想,如图①,借助四边形ABCD的面积说明了等式(a+b)c=ac+bc成立.

(1)
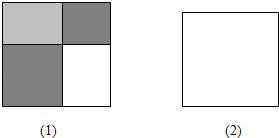
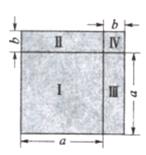
观察图②,③,找出可以推出的等式:
(2)
如图④,△ABC中,AB=BC,∠ABC=90°,BD⊥AC于点D,E是边BC上一点,作EF⊥BD于点F,EG⊥AC于点G,过A作BC的平行线交直线EG于点H.分别记△ABD,△BEF,△EGC,△AGH的面积为S1 , S2 , S3 , S4.求 的值.
的值.
等式A:(a+b)(a-b)=a2-b2:
等式B:(a+b)2=a2+2ab+b2:
可知,图②对应等式;图③对应等式.
【考点】
完全平方公式的几何背景;
平方差公式的几何背景;
矩形的判定与性质;
等腰直角三角形;
数形结合;