1.
正在建设的北京环球影城主体乐园是世界第五个环球影城乐园中既有功夫熊猫、小黄人乐园等小朋友喜欢的景区,又有过山车等深受年轻游客喜爱的游乐设施.过山车虽然惊悚恐怖,但是安全保障措施非常到位.如图所示, 为过山车的一部分轨道,它可以看成一段抛物线.其中
为过山车的一部分轨道,它可以看成一段抛物线.其中 米,
米, 米(轨道厚度忽略不计).
米(轨道厚度忽略不计).

(1)
求抛物线 的函数关系;
(2)
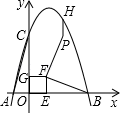
在轨道距离地面5米处有两个位置P和G,当过山车运动到G处时,平行于地面向前运动了
的函数关系;
(2)
在轨道距离地面5米处有两个位置P和G,当过山车运动到G处时,平行于地面向前运动了 米至K点,又进入下坡段
米至K点,又进入下坡段 (接口处轨道忽略不计).已知轨道抛物线
(接口处轨道忽略不计).已知轨道抛物线 的形状与抛物线
的形状与抛物线 完全相同,在G到Q的运动过程中,当过山车距地面4米时,它离出发点的水平距离最远有多远?
(3)
现需要在轨道下坡段
完全相同,在G到Q的运动过程中,当过山车距地面4米时,它离出发点的水平距离最远有多远?
(3)
现需要在轨道下坡段 进行一种安全加固,建造某种材料的水平和竖直支架
进行一种安全加固,建造某种材料的水平和竖直支架 , 且要求
, 且要求 . 已知这种材料的价格是8000元/米,如何设计支架,会使造价最低?最低造价为多少元?
. 已知这种材料的价格是8000元/米,如何设计支架,会使造价最低?最低造价为多少元?
【考点】
待定系数法求二次函数解析式;
能力提升
真题演练