1.
在学习了勾股定理后，小品对他家附近的一个公园里的音乐喷泉池产生了测量兴趣，如图，音乐喷泉池为四边形
， 在
连线上有一地方性标志物
， 据了解，修建该喷泉池时要求
， 四边形为人行观赏步道，小品通过仪器测量得到，
在
的正西方，
在的东北方向，且
， 
在的正南方150米处，恰好又在的南偏东
方向，由此他脑海里产生了以下数学问题，请你帮他解决一下．（参考数据：
， 
， 
， 
）
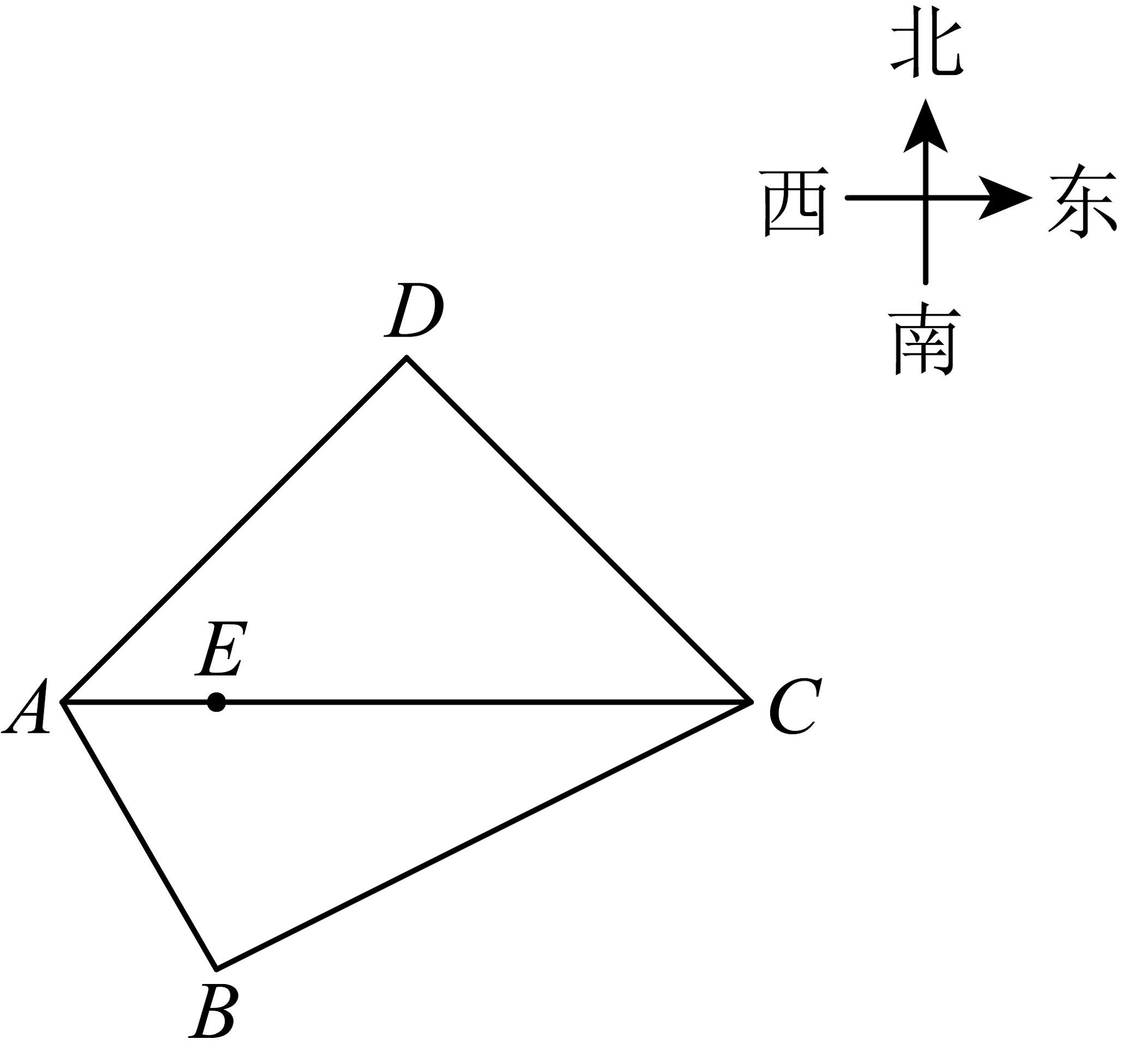
(1)
求、之间的距离（结果保留根号）；
(2)
小品和姐姐同时从点出发，沿着不同的方向到点汇合，其中小品沿着①：
的方向步行，姐姐沿着②
的方向步行，通过计算说明哪一条路更近？（结果精确到个位）
【考点】
二次根式的混合运算;
三角形内角和定理;
等腰三角形的判定与性质;
含30°角的直角三角形;
勾股定理;
