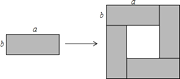
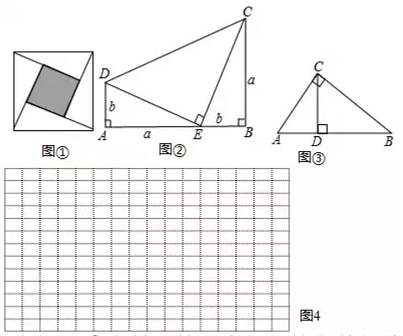
1.
根据图形直观推论或验证数学规律和公式的方法.简称为“无字证明”.例如,利用图形面积的不同计算方法,可以验证很多代数恒等式,你可以写出的代数恒等式是.(任选1图作答.回答时请注明图形序号,如图1、图2)

【考点】
完全平方公式的几何背景;
勾股定理的证明;