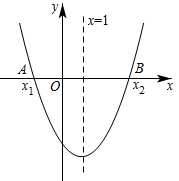
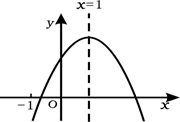
1.
已知 和
和 (
( 且
且 )是同一直角坐标系中的两条抛物线.
)是同一直角坐标系中的两条抛物线.
(1)
当 ,
,  时,求抛物线
时,求抛物线 的顶点坐标;
(2)
判断
的顶点坐标;
(2)
判断 与坐标轴的交点个数,并说明理由;
(3)
如果对于抛物线
与坐标轴的交点个数,并说明理由;
(3)
如果对于抛物线 上的任意一点
上的任意一点 均有
均有 . 当
. 当 时,求自变量
时,求自变量 的取值范围.
的取值范围.
【考点】
二次函数图象与系数的关系;
二次函数图象与坐标轴的交点问题;
二次函数与不等式(组)的综合应用;