1.
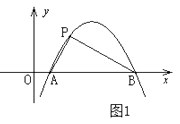
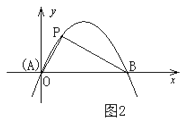
如图,抛物线 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 . 抛物线的对称轴
. 抛物线的对称轴 与经过点
与经过点 的直线
的直线 交于点
交于点 , 与
, 与 轴交于点
轴交于点 .
.

(1)
求直线 及抛物线的表达式;
(2)
在抛物线上是否存在点
及抛物线的表达式;
(2)
在抛物线上是否存在点 , 使得
, 使得 是以
是以 为直角边的直角三角形?若存在,求出所有点
为直角边的直角三角形?若存在,求出所有点 的坐标;若不存在,请说明理由;
(3)
以点
的坐标;若不存在,请说明理由;
(3)
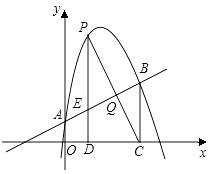
以点 为圆心,画半径为2的圆,点
为圆心,画半径为2的圆,点 为
为 上一个动点,请求出
上一个动点,请求出 的最小值.
的最小值.
【考点】
待定系数法求二次函数解析式;
二次函数-动态几何问题;
相似三角形的判定-AA;
能力提升