0 返回出卷网首页
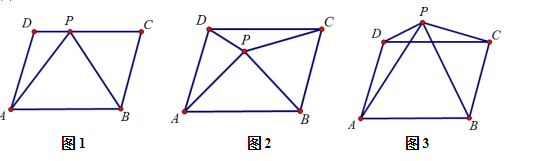
1. 定义：若端点均在四边形边上的线段平分该四边形的面积，则我们称这条线段为该四边形的等积线。例：如图1，在□ABCD中，连结AC，我们可以利用“夹在两条平行线间的垂线段相等”，结合“等底（同底）等高的两个三角形面积相等”来说明△ABC与△ADC的面积相等，即AC是□ABCD的等积线.

(1) 请利用图1完成例的证明.
(2) 如图2，在四边形ABCD中，连结AC，BD，已知点D与BC上一点E的连线段DE是四边形ABCD的等积线，过点E作BD的平行线，交AC于点F，若AC=6，求 CF的长度.
(3) 如图3，在（2）的条件下，延长EF，交CD于点G.若FG=EF，请在图中找出一条不同于DE的四边形ABCD的等积线，并说明理由.
【考点】
平行线的性质; 三角形的面积; 平行四边形的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
真题演练
换一批
1. 如图1 ，已知平行四边形 ， 是 的角平分线，交 于点E．

 

(1) 求证： ．
(2) 如图2所示，点P是平行四边形 的边 所在直线上一点，若 ，且 ， ，求 的面积．
综合题 普通
2. 如果一条直线把一个平面图形的面积分成相等的两部分，我们把这条直线称为这个平面图形的一条面积等分线．
(1) 平行四边形有条面积等分线；
(2) 如图，四边形ABCD中，AB与CD不平行，AB≠CD，且S△ABC＜S△ACD ， 过点A画出四边形ABCD的面积等分线，并写出理由
综合题 普通
3.   如图，
(1) 如图 1，若 P是口ABCD 边 CD 上任意一点，连结 AP、BP，若△APB 的面积为 60 ，△APD的面积为 18，则 S△APC=.
(2) 如图 2，①若点 P 运动到口ABCD 内一点时，试说明 S△APB +S△DPC =S△BPC +S△APD.

②若此时△APB 的面积为 60，△APD 的面积为 18，则 S△APC=.
(3) 如图3，①利用（2）中的方法你会发现，S△APB ，S△DPC ，S△BPC ，S△APD 之间存在怎样的关系：.

②若此时△APB 的面积为 60，△APD 的面积为 18，请利用你的发现，求 S△APC 的面积？
综合题 困难