如图，

0 返回出卷网首页

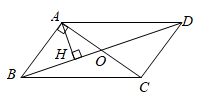
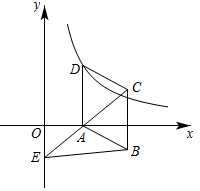
1. 如图，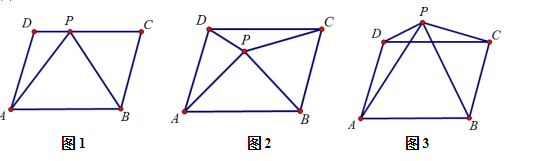

(1) 如图 1，若 P是口ABCD 边 CD 上任意一点，连结 AP、BP，若△APB 的面积为 60 ，△APD的面积为 18，则 S△APC=.

(2) 如图 2，①若点 P 运动到口ABCD 内一点时，试说明 S△APB +S△DPC =S△BPC +S△APD.

②若此时△APB 的面积为 60，△APD 的面积为 18，则 S△APC=.

(3) 如图3，①利用（2）中的方法你会发现，S△APB ，S△DPC ，S△BPC ，S△APD 之间存在怎样的关系：.

②若此时△APB 的面积为 60，△APD 的面积为 18，请利用你的发现，求 S△APC 的面积？

【考点】

三角形的面积; 平行四边形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图1 ，已知平行四边形 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的角平分线，交 $\text{[math]}$ 于点E．

(1) 求证： $\text{[math]}$ ．

(2) 如图2所示，点P是平行四边形 $\text{[math]}$ 的边 $\text{[math]}$ 所在直线上一点，若 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积．

综合题普通

2. 如果一条直线把一个平面图形的面积分成相等的两部分，我们把这条直线称为这个平面图形的一条面积等分线．

(1) 平行四边形有条面积等分线；

(2) 如图，四边形ABCD中，AB与CD不平行，AB≠CD，且S_△ABC＜S_△ACD ，过点A画出四边形ABCD的面积等分线，并写出理由

综合题普通

3. 正方形网格中的每个小正方形边长都是1，

(1) 请在图中画出等腰△ABC ，使AB＝AC＝ $\text{[math]}$ ，BC＝ $\text{[math]}$ ；

(2) 在△ABC中，AB边上的高为．

综合题普通