1.
在平面直角坐标系 中,
中, 的半径为1.对于
的半径为1.对于 外的一点
外的一点 和弦
和弦 , 给出如下定义:若点
, 给出如下定义:若点 在直线
在直线 上,点
上,点 在
在 上,使得
上,使得 的最大值为
的最大值为 , 则称点
, 则称点 是弦
是弦 的“
的“ 关联点”.
关联点”.

(1)
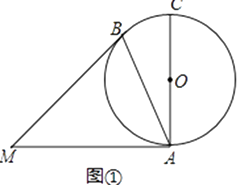
如图,点 ,
,  ,
,  (2)
已知
(2)
已知 是直线
是直线 上一点,且存在
上一点,且存在 的弦
的弦 , 使得点
, 使得点 是弦
是弦 的“
的“ 关联点”.记点
关联点”.记点 的横坐标为
的横坐标为 , 直接写出
, 直接写出 的取值范围.
的取值范围.
①弦的“
关联点”的坐标是________;
②若点是弦
的“
关联点”,求
的值;
【考点】
垂径定理;
切线的性质;
解直角三角形;
坐标系中的两点距离公式;
能力提升