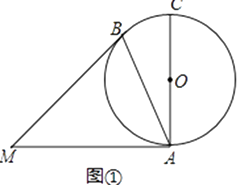
筒车是我国古代利用水利驱动的灌溉工具，如图所示，筒车按逆时针方向，每秒钟转，筒车与水面分别交于A，B．，筒车的轴心O 距离水面的高度长为，筒车上均匀分布着若干个盛水筒，若以某个盛水筒 P刚浮出水面时开始计算时间．

0 返回出卷网首页

1. 筒车是我国古代利用水利驱动的灌溉工具，如图所示，筒车 $\text{[math]}$ 按逆时针方向，每秒钟转 $\text{[math]}$ ，筒车与水面分别交于A，B． $\text{[math]}$ ，筒车的轴心O 距离水面的高度 $\text{[math]}$ 长为 $\text{[math]}$ ，筒车上均匀分布着若干个盛水筒，若以某个盛水筒 P刚浮出水面时开始计算时间．

(1) 求筒车 $\text{[math]}$ 的半径；

(2) 求出筒车 $\text{[math]}$ 在水面下弓形的面积；

(3) 若接水槽 $\text{[math]}$ 所在直线是 $\text{[math]}$ 的切线，且与直线 $\text{[math]}$ 交于点M． $\text{[math]}$ ，求盛水筒P从最高点开始，至少经过多长时间恰好在直线 $\text{[math]}$ 上？（参考数据 $\text{[math]}$ ， $\text{[math]}$ ）

【考点】

垂径定理; 切线的性质; 解直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 已知⊙O中，AC为直径，MA、MB分别切⊙O于点A、B．

(1) 如图①，若∠BAC=23°，求∠AMB的大小；

(2) 如图②，过点B作BD∥MA，交AC于点E，交⊙O于点D，若BD=MA，求∠AMB的大小．

解答题普通

2. 如图，AB是⊙O的切线，A为切点，AC是⊙O的弦，过点O作OH⊥AC于点H．若OH=2，AB=12，OB=13．求：

(1) ⊙O的半径．

(2) AC的长．

解答题普通

3. 如图，半径为1的 $\text{[math]}$ 在矩形 $\text{[math]}$ 的内部，将圆周12等分，过各等分点作圆的切线，在第一条切线上量取 $\text{[math]}$ ， $\text{[math]}$ 为图的周长，在第二条切线上量取 $\text{[math]}$ ，在第三条切线上量取 $\text{[math]}$ ，在第四条切线上量取 $\text{[math]}$ ，依此类推，将 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 用光滑的曲线连结，若此时 $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 所在直线恰好经过点 $\text{[math]}$ ，求边 $\text{[math]}$ 的长．

解答题困难