1.
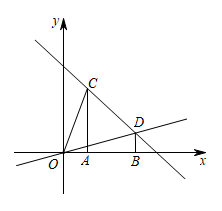
如图1， 在平而直角坐标系中，直线AB：y= 
x+4与坐标轴交于A，B两点，点C为AB的中点，动点P从点A出发，沿AO方向以每秒1个单位的速度向终点O运动，同时动点Q从点O出发，以每秒2个单位的速度沿射线OB方向运动，当点P到达点O时，点Q也停止运动．以CP，CQ为邻边构造 
CPDQ，设点P运动的时间为t秒．
(1)
直接写出点C的坐标为；
(2)
如图2，过点D作DG⊥y轴，过点C作CH⊥x轴．证明：△PDG≌△CQH；
(3)
如图3，连结OC，当点D恰好落在△OBC的边所在的直线上时，求所有满足要求的t的值．
【考点】
待定系数法求一次函数解析式;
平行线的性质;
平行四边形的性质;
三角形全等的判定-AAS;
