1.
如图1,在平面直角坐标系中,点 ,
,  ,
,  ,
,  ,
,  满足
满足 .
.

(1)
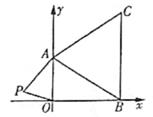
如图1,点 的坐标为,点
的坐标为,点 的坐标为;
(2)
如图1,已知坐标轴上有两个动点
的坐标为;
(2)
如图1,已知坐标轴上有两个动点 、
、 , 点
, 点 从
从 点出发沿
点出发沿 轴负方向以
轴负方向以 个单位每秒的速度移动,点
个单位每秒的速度移动,点 从
从 点出发沿
点出发沿 轴负方向以
轴负方向以 个单位每秒的速度移动,设运动时间为
个单位每秒的速度移动,设运动时间为 秒.当三角形
秒.当三角形 的面积与三角形
的面积与三角形 的面积之和等于
的面积之和等于 时,求
时,求 的值.
(3)
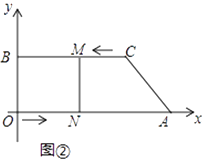
如图2,过点
的值.
(3)
如图2,过点 作
作 轴的平行线
轴的平行线 , 点
, 点 是线段
是线段 上一个动点(不与
上一个动点(不与 、
、 重合),连接
重合),连接 ,
,  平分
平分 ,
,  平分
平分 交
交 于点
于点 , 过点
, 过点 作
作 交
交 于点
于点 , 问
, 问 的值是否会发生变化?若不变,请求出它的值:若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值:若变化,请说明理由.
【考点】
三角形的面积;
偶次方的非负性;
算术平方根的性质(双重非负性);
平行线的判定与性质的应用-证明问题;
平行公理的推论;
能力提升