1.
已知平行四边形 ,
,  , 点E为对角线
, 点E为对角线 上一动点,连接
上一动点,连接 , 以
, 以 为一边在
为一边在 的右侧作
的右侧作 , 使
, 使 , 连接
, 连接 .
.

(1)
若 且
且 , 当
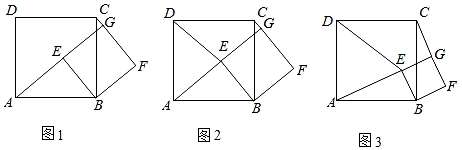
, 当 , 如图①,求此时
, 如图①,求此时 度数;
(2)
若
度数;
(2)
若 且
且 , 当
, 当 ,
,  时,如图②,判断C,D,F三点是否共线并说明理由;
(3)
如图③若
时,如图②,判断C,D,F三点是否共线并说明理由;
(3)
如图③若 ,
,  且
且 ,
,  , 当
, 当 是以
是以 为底的等腰三角形时,直接写出
为底的等腰三角形时,直接写出 的面积.
的面积.
【考点】
正方形的判定与性质;
四边形的综合;
手拉手全等模型;
同侧一线三垂直全等模型;
能力提升