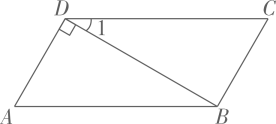
请将下列证明过程补充完整：如图，已知，，，求证：．证明：，；；∴ （同位角相等，两直线平行）；∴ ；∵（已知）；∴ ；∴（）；∴（）．

0 返回出卷网首页

1. 请将下列证明过程补充完整：如图，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ．

证明： $\text{[math]}$ ， $\text{[math]}$ ；

$\text{[math]}$ ；

∴ $\text{[math]}$ （同位角相等，两直线平行）；

∴ $\text{[math]}$ ；

∵ $\text{[math]}$ （已知）；

∴ $\text{[math]}$ ；

∴ $\text{[math]}$ （）；

∴ $\text{[math]}$ （）．

【考点】

垂线的概念; 平行线的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

证明题普通

1. 完成下面的证明．

如图，在三角形 $\text{[math]}$ 中， $\text{[math]}$ 于点F．点G，D，E分别在边 $\text{[math]}$ 上，且 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 互补，求证： $\text{[math]}$ ．

证明：∵ $\text{[math]}$ ，

∴ $\text{[math]}$ （）

∴ $\text{[math]}$ （）

∵ $\text{[math]}$ 与 $\text{[math]}$ 互补，

∴ $\text{[math]}$ （补角的定义）．

∴ $\text{[math]}$ $\text{[math]}$ （等量代换）．

∴ $\text{[math]}$ （）．

∴ $\text{[math]}$ （）

∵ $\text{[math]}$ ，

∴ $\text{[math]}$ （垂直的定义）．

∴ $\text{[math]}$ （等量代换）．

∴ $\text{[math]}$ ．

证明题容易

2. 阅读下列推理过程，在括号中填写理由．

如图，已知在三角形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$ ．

证明： $\text{[math]}$ （），

$\text{[math]}$ （），

$\text{[math]}$ （），

$\text{[math]}$ （），

$\text{[math]}$ （），

$\text{[math]}$ （），

$\text{[math]}$ （），

$\text{[math]}$ （），

$\text{[math]}$ ．

$\text{[math]}$ （）．

$\text{[math]}$ （）．

证明题容易

3. 请结合题意，在横线上填上合适的推理依据．

已知：如图， $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ．

证明： $\text{[math]}$ （已知）

∴ $\text{[math]}$ （垂直的定义）

$\text{[math]}$ （已知）

$\text{[math]}$ $\text{[math]}$ （）

$\text{[math]}$ （）

又∵ $\text{[math]}$ （已知）

∴ $\text{[math]}$ （）

$\text{[math]}$ （）

∴ $\text{[math]}$ （两直线平行，同位角相等）

$\text{[math]}$ ．（）

证明题容易