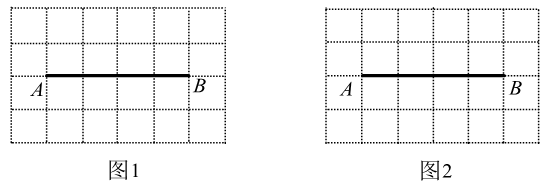
1.
在平面直角坐标系 中,将过
中,将过 轴上的点
轴上的点 , 且平行于
, 且平行于 轴的直线,记作直线
轴的直线,记作直线 . 对于图形
. 对于图形 和
和 , 若存在直线
, 若存在直线 , 使得图形
, 使得图形 关于
关于 的对称图形都在图形
的对称图形都在图形 内(包括边界),则称图形
内(包括边界),则称图形 是图形
是图形 的一阶
的一阶 包含图形.若存在直线
包含图形.若存在直线 与直线
与直线 且
且 , 图形
, 图形 关于直线
关于直线 的对称图形记为图形
的对称图形记为图形 , 图形
, 图形 关于
关于 的对称图形都在图形
的对称图形都在图形 内(包括边界),则称图形
内(包括边界),则称图形 是图形
是图形 的二阶
的二阶 ,
,  包含图形,记
包含图形,记 为图形
为图形 关于图形
关于图形 的包含轴距.
的包含轴距.

已知 ,
,
,
,
(1)
若 ,
(2)
若点
,
(2)
若点 为四边形
为四边形 的二阶
的二阶 , 1包含图形,则
, 1包含图形,则 的取值范围是______;
(3)
当
的取值范围是______;
(3)
当 时,若
时,若 ,
,  ,
,  是四边形
是四边形 的二阶
的二阶 ,
,  包含图形,则
包含图形,则 的最大值与最小值的差是______.
的最大值与最小值的差是______.
①是线段
的一阶
包含图形,则
______;
②是线段
的一阶
包含图形,则
的取值范围是______;
【考点】
勾股定理;
正方形的判定;
能力提升
真题演练