1.


(1)
问题提出:
(2)
问题探究:
(3)
问题解决:
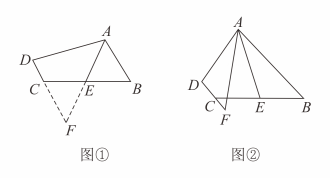
我们把两个面积相等但不全等的三角形叫做“偏等积三角形”.如图1,中,
,
为AC上一点,当
▲ 时,
与
是偏等积三角形;
如图2,与
是偏等积三角形,
, 且线段AD的长度为正整数,过点
作
交AD的延长线于点
, 则
▲ ;
如图3,四边形ABED是一片绿色花园,是等腰直角三角形,
.
①与
是偏等积三角形吗?请说明理由;
②已知的面积为
. 如图4,计划修建一条经过点
的笔直的小路CF , F在BE边上,FC的延长线经过AD中点
. 若小路每米造价500元,请计算修建小路的总造价为 ▲ .
【考点】
三角形的面积;
三角形三边关系;
全等三角形的应用;
三角形全等的判定-AAS;
三角形的综合;
能力提升