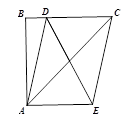
如图，在中，，，，点P为BC边上任意一点，连接PA，将PA沿BC方向平移至CQ，连接AQ、PQ，则当PQ取得最小值时，BP的长为（）

0 返回出卷网首页

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点P为BC边上任意一点，连接PA，将PA沿BC方向平移至CQ，连接AQ、PQ，则当PQ取得最小值时，BP的长为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. 2

【考点】

垂线段最短及其应用; 平行四边形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题困难

1. 如图，体育课上测量跳远成绩的依据是（）

A. 平行线间的距离相等 B. 垂线段最短 C. 两点之间，线段最短 D. 两点确定一条直线

单选题容易

2. 如图，四边形 $\text{[math]}$ 是平行四边形，对角线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，则下列判断正确的是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 在平行四边形 $\text{[math]}$ 中，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易