1.
【项目主题】合理设计,实用便民
【项目背景】为了提升交通安全,南山某城市隧道入口进行道路设施规划,计划安装车道指示灯.现需要对隧道入口隔音屏顶部的装灯位置进行合理设计.某数学兴趣小组成员开展了如下探究活动:
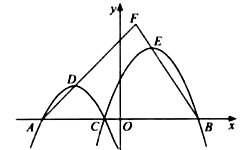
素材1 | 图1是隧道入口隔音屏,其顶部轮廓可近似的看成抛物线,其截面如图2所示.以地面为 |
素材2 | 为测量素材1的点 |
素材3 | 为提高通行效率,需在隔音屏顶部加装灯架,为每个车道增设指示灯.按要求,指示灯需距离地面 |

根据提供素材,完成下列问题:
(1)
数学小组计算出 的长度,具体如下:
的长度,具体如下:
(2)
根据已知条件,求出抛物线 的解析式(不需要写出x的取值范围).
(3)
求出素材3中l的值,并判断
的解析式(不需要写出x的取值范围).
(3)
求出素材3中l的值,并判断 长的材料能否完成灯架和支架的安装.
长的材料能否完成灯架和支架的安装.
解:设
又
|
请补全上述求解过程中①②③所缺的内容:
【考点】
待定系数法求二次函数解析式;
相似三角形的判定与性质;
相似三角形的应用;
能力提升