1.
【问题呈现】小华遇到这样一个问题,如图1, 中,
中, ,
,  ,
,  , 在
, 在 内部有一点
内部有一点 , 连接
, 连接 、
、 、
、 , 求
, 求 的最小值.
的最小值.
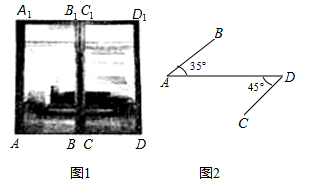
【问题解决】小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将绕点
顺时针旋转
, 得到
, 连接
、
, 则
的长即为所求.

(1)
请你写出图2中, 的最小值为______;
(2)
【类比应用】如图3,直角坐标系中有菱形
的最小值为______;
(2)
【类比应用】如图3,直角坐标系中有菱形 , 点
, 点 与原点重合,
与原点重合, 坐标为
坐标为 ,
,  , 若在菱形
, 若在菱形 内部有一动点
内部有一动点 , 试求
, 试求 的最小值,并求出此时点
的最小值,并求出此时点 的坐标是多少;
(3)
【生活实际】如图4,一个矩形菜地的
的坐标是多少;
(3)
【生活实际】如图4,一个矩形菜地的 三个顶点处建有三个菜窖,现打算在矩形菜地内部建一个蔬菜运输点
三个顶点处建有三个菜窖,现打算在矩形菜地内部建一个蔬菜运输点 , 经研究发现,运输点
, 经研究发现,运输点 到
到 三个菜窖的总路程至少为
三个菜窖的总路程至少为 千米,若
千米,若 , 则此矩形菜地的面积至少为______平方千米.
, 则此矩形菜地的面积至少为______平方千米.
【考点】
等边三角形的判定与性质;
勾股定理;
解直角三角形;
旋转的性质;
能力提升
真题演练