0 返回出卷网首页
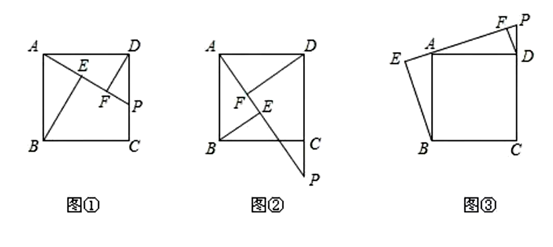
1. 如图，正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上，连接BF、DF、CF

(1) 求证：BF=DF；
(2) 设AB=1，AE=a（0＜a＜1）是否存在a的值，使得正方形AEFG的面积等于梯形BEFC的面积？若存在，求出a的值；若不存在，说明理由．
【考点】
全等三角形的判定与性质; 正方形的性质; 梯形;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
换一批
1. 在正方形ABCD中，AB＝AD，∠BAD＝90°，P是CD边上一点，连结PA，分别过点B，D作BE⊥PA，DF⊥PA，垂足分别为点E，F，如图①

(1) 求证：BE＝DF＋EF；
(2) 若点P在DC的延长线上，如图②，上述结论还成立吗？如果成立请写出证明过程；如果不成立，请写出正确结论并加以证明.
(3) 若点P在CD的延长线上，如图③，那么这三条线段的数量关系是.(直接写出结果)
综合题 困难
2. 如图，在正方形ABCD中，AB=BC=CD=AD，∠BAD=∠B=∠C=∠D=90°，点E、F分别在正方形ABCD的边DC、BC上，AG⊥EF且 AG=AB，垂足为G，则：

(1) △ABF与△ AGF全等吗？说明理由；
(2) 求∠EAF的度数；
(3) 若AG=4，△AEF的面积是7，求△CEF的面积．
综合题 普通
3. 四边形ABCD是正方形（提示：正方形四边相等，四个角都是90°）

(1) 如图1，点G是BC边上任意一点（不与点B、C重合），连接AG，作BF⊥AG于点F，DE⊥AG于点E．

求证：△ABF≌△DAE；
(2) 直接写出（1）中，线段EF与AF、BF的等量关系；
(3) ①如图2，若点G是CD边上任意一点（不与点C、D重合），连接AG，作BF⊥AG于点F，DE⊥AG于点E，则图中全等三角形是，线段EF与AF、BF的等量关系是；

②如图3，若点G是CD延长线上任意一点，连接AG，作BF⊥AG于点F，DE⊥AG于点E，线段EF与AF、BF的等量关系是；
(4) 若点G是BC延长线上任意一点，连接AG，作BF⊥AG于点F，DE⊥AG于点E，请画图、探究线段EF与AF、BF的等量关系．
综合题 困难