1.
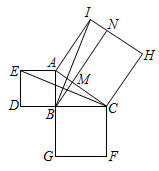
如图,在正方形ABCD中,AB=4,点E在对角线AC上,连接BE、DE,

(1)
如图1,作EM⊥AB交AB于点M,当AE=  时,求BE的长;
(2)
如图2,作EG⊥BE交CD于点G,求证:BE=EG;
(3)
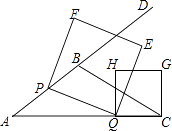
如图3,作EF⊥BC交BC于点F,设BF=x,△BEF的面积为y.当x取何值时,y取得最大值,最大值是多少?当△BEF的面积取得最大值时,在直线EF取点P,连接BP、PC,使得∠BPC=45°,求EP的长度.
时,求BE的长;
(2)
如图2,作EG⊥BE交CD于点G,求证:BE=EG;
(3)
如图3,作EF⊥BC交BC于点F,设BF=x,△BEF的面积为y.当x取何值时,y取得最大值,最大值是多少?当△BEF的面积取得最大值时,在直线EF取点P,连接BP、PC,使得∠BPC=45°,求EP的长度.
【考点】
勾股定理;
正方形的性质;
二次函数的实际应用-几何问题;
能力提升
真题演练