0 返回出卷网首页
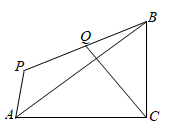
1. 如图，在四边形ABCD中，∠ABC=90° ，AC=AD ， M ， N分别为AC ， CD的中点，连接BM ， MN ， BN.

(1) 求证：BM=MN；
(2) 若∠BAD=60°，AC平分 ，AC=2， 写出求BN长的思路.
【考点】
勾股定理; 三角形的中位线定理; 直角三角形斜边上的中线;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．

(1) 求证：BM=MN；
(2) ∠BAD=60°，AC平分∠BAD，AC=2，求BN的长．
综合题 普通
2. 如图1，在矩形ABCD中，AB=4，BC=3，点E为边CD上一动点，连结AE，作点D关于直线AE的对称点F，连结EF，DF，CF，AF，DF与AE交于点G．

(1) 若DE=2，求证：AE//CF．
(2) 如图2，连结AC，BD，若点F在矩形ABCD的对角线上，求所有满足条件的DE的长．
(3) 如图3，连结BF，当点F到矩形ABCD一个顶点的距离等于2时，请直接写出△BCF的面积．
综合题 困难
3. 定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．

请解决下列问题：

(1) 已知点M，N是线段AB的勾股分割点，且BN＞MN＞AM．若AM=2，MN=3，求BN的长；
(2) 如图2，若点F、M、N、G分别是AB、AD、AE、AC边上的中点，点D，E是线段BC的勾股分割点，且EC＞DE＞BD，求证：点M，N是线段FG的勾股分割点．
综合题 普通