1.
从反思中总结基本活动经验是一个重要的学习方法.例如,我们在全等学习中所总结的“一线三等角、K型全等”这一基本图形,可以使得我们在观察新问题的时候很自然地联想,借助已有经验,迅速解决问题.
(1)
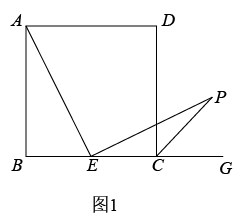
如图1,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,且MN=DM.
(2)
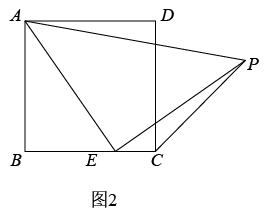
如果(1)的条件去掉“且MN=DM”,加上“交∠CBE的平分线与点N”,如图2,求证:MD = MN.如何获得问题的解决,不妨在OD上取一点G,连接MG,设法构造△MDG与△NMB全等,请你按此思路证明:MD = MN.
(3)
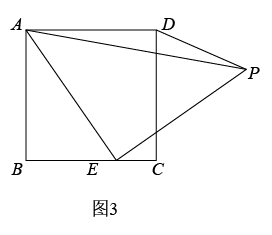
如图3,(2)的条件下请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,请你指出正确的结论,并给出证明.
设OM=a,请你利用基本活动经验直接写出点N的坐标(用含a的代数式表示);



【考点】
三角形全等的判定;
等腰三角形的性质;
正方形的性质;
能力提升
真题演练