在四边形OABC中，AB∥OC，∠OAB＝90°， ∠OCB＝60°，AB＝2，OA＝2 .

0 返回出卷网首页

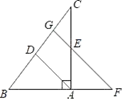
1. 在四边形OABC中，AB∥OC，∠OAB＝90°， ∠OCB＝60°，AB＝2，OA＝2 $\text{[math]}$ .

(1) 如图①，连接OB，请直接写出OB的长度；

(2) 如图②，过点O作OH⊥BC于点H.动点P从点H出发，沿线段HO向点O运动，动点Q从点O出发，沿线段OA向点A运动，两点同时出发，速度都为每秒1个单位长度，设点P运动的时间为t秒，△OPQ的面积为S(平方单位)．

①求S与t之间的函数关系式；

②设PQ与OB交于点M，当△OPM为等腰三角形时，试求出△OPQ的面积S的值．

【考点】

平行线的性质; 三角形的面积; 等腰三角形的性质; 勾股定理; 锐角三角函数的定义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 问题探究

(1) 请在图①、图② 各作两条直线，使它们将正方形ABCD与半⊙O的面积三等分；

(2) 如图③，在矩形ABCD中，AB＝3，BC＝4，请在图③中过顶点A作两条直线，使它们将矩形ABCD的面积三等分，并说明理由；

问题解决

(3) 位于宝鸡市凤翔区的机场将计划于2024年建成通航．如图④，在机场旁边有一块平行四边形ABCD空地，其中AB＝AC＝100米，BC＝120米，根据视觉效果和花期特点，机场设计部门想在这块空地上种上等面积的三种不同的花，要求从入口点A处修两条笔直的小路（小路面积忽略不计）方便旅客赏花，两条小路将这块空地的面积三等分．那么设计部门能否实现自己的想法？若能实现，请通过计算，画图说明；若不能，请说明理由．

综合题普通

2. 如图，在Rt△ABC中，∠BAC＝90°，AD平分∠BAC，过AC的中点E作FG∥AD，交BA的延长线于点F，交BC于点G，

(1) 求证：AE＝AF；

(2) 若BC＝ $\text{[math]}$ AB，AF＝3，求BC的长.

综合题普通

3. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，D是边AB的中点，动点P在线段BA上且不与点A ， B ， D重合，以PD为边构造 $\text{[math]}$ ，使 $\text{[math]}$ ， $\text{[math]}$ ，且点Q与点C在直线AB同侧，设 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 重叠部分图形的面积为S ．

(1) 当点Q在边BC上时，求BP的长；

(2) 当 $\text{[math]}$ 时，求S关于x的函数关系式.

综合题困难