如图，正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上（点P与A、C不重合），QP与BC交于E，QP延长线与AD交于点F，连接CQ．

0 返回出卷网首页

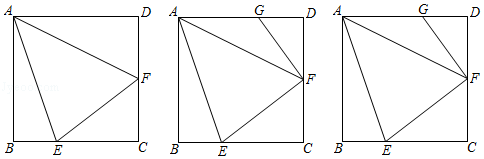
1. 如图，正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上（点P与A、C不重合），QP与BC交于E，QP延长线与AD交于点F，连接CQ．

(1) ①求证：AP=CQ；②求证：PA²=AF•AD；

(2) 若AP：PC=1：3，求tan∠CBQ．

【考点】

全等三角形的判定与性质; 正方形的性质; 相似三角形的判定与性质; 解直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知：如图1，在面积为3的正方形ABCD中，E，F分别是BC和CD边上的两点，AE⊥BF于点G，且BE=1．

(1) 求证：△ABE≌△BCF；

(2) 求出△ABE和△BCF重叠部分（即△BEG）的面积；

(3) 现将△ABE绕点A逆时针方向旋转到△AB′E′（如图2），使点E落在CD边上的点E′处，问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化？请说明理由．

综合题普通

2. 已知：如图，四边形ABCD是正方形，点E、F分别在BC、CD上，连接AE、EF、AF，且∠DAE＝∠AEF．

(1) 求证：EF＝BE+DF；

(2) 线段AF的垂直平分线交AD于点G，连接FG，求证：∠EFG＝90°；

(3) 在（2）的条件下，若tan∠DFG＝ $\text{[math]}$ ，EF＝ $\text{[math]}$ ，求S_△AEF ．

综合题普通

3. 如图，在正方形ABCD中，AB=6，E为AC上一点，以AE为直角边构造等腰直角△AEF(点F在AB左侧)，分别延长FB，DE交于点H，DH交线段BC于点M，连结BE。

(1) 求证：△AFB≌△AED

(2) 当AE=4 $\text{[math]}$ 时，求tan∠MBH的值。

(3) 当点H关于直线BE的对称点落在△ABC的边上时，求∠EBC的度数。

(4) 若△BEH与△DEC的面积相等，记△EMC与△ABE的面积分别为S₁ ， S₂ ，则 $\text{[math]}$ 的值为。(直接写出答案)

综合题困难