1.
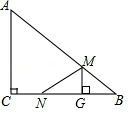
如图,已知△ABC的顶点坐标分别为A(3,0),B(0,4),C(-3,0)。动点M,N同时从A点出发,M沿A→C,N沿折线A→B→C,均以每秒1个单位长度的速度移动,当一个动点到达终点C时,另一个动点也随之停止移动,移动时间记为t秒。连接MN。

(1)
求直线BC的解析式;
(2)
移动过程中,将△AMN沿直线MN翻折,点A恰好落在BC边上点D处,求此时t值及点D的坐标;
(3)
当点M,N移动时,记△ABC在直线MN右侧部分的面积为S,求S关于时间t的函数关系式。
【考点】
待定系数法求一次函数解析式;
翻折变换(折叠问题);
相似三角形的判定与性质;
二次函数的实际应用-几何问题;
三角形-动点问题;
能力提升