1.
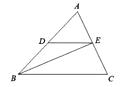
如图,在△ABC中,点D在AB边上,DE∥BC,与边AC交于点E,连结BE,记△ADE,△BCE的面积分别为S1 , S2 , ( )
A.
若  ,则
,则  B.
若
B.
若  ,则
,则  C.
若
C.
若  ,则
,则  D.
若
D.
若  ,则
,则 
【考点】
三角形的面积;
两条直线被一组平行线所截,所得的对应线段成比例;